“Mechanistic links between cellular trade-offs, gene expression and growth”
Andrea Weisse
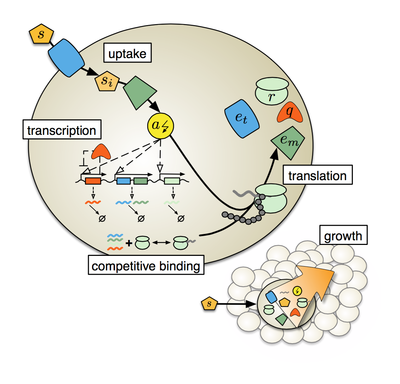
Cells have finite resources. Committing resources to one task thus reduces the amount of resource available to other tasks. Intracellular processes consequently do not work in isolation but continually interact with the rest of the cell.
Here we consider three trade-offs that because of limitations in levels of cellular energy, free ribosomes, and proteins are faced by all living cells and construct a mathematical model that comprises these trade-offs. Our model describes the mechanisms of protein synthesis and how cells extract resources from their environment. It further couples gene expression with growth rate and growth rate with a growing population of cells. The model recovers Monod's law for the growth of microbes and two other empirical relationships connecting growth rate to the mass fraction of ribosomes.
As trade-offs are experienced by all cells and because growth largely determines cellular fitness, a predictive understanding of how biochemical processes affect others and affect growth is important for diverse applications. We can explain growth-related effects in gene dosage compensation by paralogs and predict host–circuit interactions in synthetic biology. Simulating competitions between strains, we find that the regulation of metabolic pathways may have evolved not to match expression of enzymes to levels of extracellular substrates in changing environments but rather to balance a trade-off between exploiting one type of nutrient over another. Although coarse-grained, the trade-offs that the model embodies are fundamental, and, as such, our modeling framework has potentially wide application, including in both biotechnology and medicine.
"Dynamic modelling of physiological processes related to energy allocation in aquatic invertebrates – Towards a better environmental risk assessment."
S. Charles & C. Lopes
Aquatic ecosystems suffer from various toxic pressures, mainly from anthropic origin. The ecological impacts of this environmental contamination are primarily assessed based on the quantification of the effects at the individual level. These effects are then extrapolated to higher levels of biological organization (population, community, ecosystem), i.e. the final targets to protect as defined by regulators.
The Dynamic Energy Budget (DEB) theory translates into mechanistic models the way individuals allocate their energy to the key physiological processes of their life cycle: growth, maintenance and reproduction. Under toxic pressure, the energy allocation can be modified, leading for example to a decrease in the food assimilation rate or to an energy overconsumption. DEBtox equations are proposed as an extension of DEB models to describe the potential changes in individual life history traits due to the presence of contaminants in the environment, according to various assumptions on their mode of action.
We will illustrate how DEB and DEBtox models can successfully be used to describe life history traits of two aquatic invertebrates (the cladoceran Daphnia magna and the amphipod Gammarus fossarum) submitted to disturbed conditions. We will show how DEB models can be adapted according to the biological and the physiological characteristics of the studied species. Then we will show how dynamical matrix models may be helpful in predicting consequences at the population level by integrating the effects modelled at the individual level.
"Dynamical Allocation of Cellular Resources as an Optimal Control Problem: Novel Insights into Microbial Growth Strategies"
Niels Giordano
Studies of microbial physiology have resulted in so-called growth laws, empirical regularities that relate the growth rate to the macromolecular composition of the cell. Theoretical work has shown that the growth laws can be derived from coarse-grained models of resource allocation. Moreover, control strategies enabling microorganisms to optimize the growth rate over a range of conditions
have been described.
While the existing literature has mainly focused on steady-state conditions, these are rarely found in natural habitats of microorganisms, where the environment is continually changing. The aim of this paper is to generalize the study of microbial growth strategies from steady-state conditions to dynamical environments, using a resource allocation model of the cell. We formulate dynamic growth maximization as an optimal control problem and solve this problem using Pontryagin’s Maximum Principle, resulting in a so-called bang-bang singular solution. We compare this theoretical gold standard with different possible implementations of growth control in bacterial cells. We find that control strategies enabling growth-rate maximization at steady state are not necessarily optimal when considering transitions from one growth regime to another, for example by shifting bacterial cells to a medium supporting a higher growth rate. Moreover, the control strategy approaching the theoretical optimum under dynamic conditions requires information on several rather than a single physiological variable. Interestingly, this near-optimal strategy has structural analogies with the regulation of ribosomal protein synthesis by ppGpp in Escherichia coli. Our results illustrate the interest of methods from control engineering for better understanding the principles underlying resource allocation in microorganisms.
Donwload SeMoVi poster here

